A estatística descritiva é um conjunto de técnicas que visa organizar e resumir os dados de forma clara e objetiva.
Diferentemente da estatística inferencial, que pega uma amostra dos dados de uma população para estimar os valores, a estatística descritiva vai se concentrar em descrever a interpretar as características principais do conjunto.
No artigo de hoje iremos explorar sobre a estatística descritiva, citar os principais usos, medidas e importância.
Sirva-se com seu cafezinho ou chá, e vamos para mais uma rodada de conhecimento!
Importância da Estatística descritiva na Análise de dados
Para o mundo dos dados, que tem se tornado cada vez maior, a estatística descritiva mostrou-se uma ferramenta indispensável.
Por meio dela, conseguimos identificar padrões e tendência, tomar decisões baseadas em evidências, comunicar resultados, detectar anomalias e muito mais!
Principais medidas da estatística descritiva
Agora que sabemos o que é a estatística descritiva e sua utilidade no mundo dos dados podemos conhecer algumas de suas principais medidas
Medidas de tendência central
Aqui nosso objetivo e identificar o centro de uma distribuição de dados, as principais medidas são a média, mediana e a moda, cada uma com uma perspectiva diferente sobre os dados.
Média aritmética
O objetivo principal da média aritmética é representar o valor médio de um conjunto de dados.
Ela é calculada pela soma de todos os valores divididas pelo número de observações.
Exemplo:
Um professor tem uma turma com 10 alunos e deseja saber a média de idade deles.
Diante disso, ele anotou suas idades e nomes no Excel:
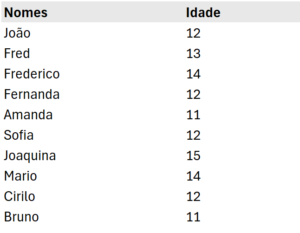
Soma das idades: 126
Número de alunos: 10
Dividimos soma por número de alunos e temos que a média de idade é aproximadamente de 12 anos.
A desvantagem da média é que ele é sensível a Outliers.
Ou seja, caso tivéssemos uma idade muito alta ou muito baixa nessa base, a média seria diretamente influenciada, prejudicando o resultado.
Mediana
Mediana é o valor que divide o conjunto de dados em duas partes iguais, ela é ideal para situações em que se tem outliers, pois é considerada uma medida robusta (menos sensível a outliers).
Exemplo:
Vamos considerar uma situação em que se tem um aluno de 100 anos na sala.
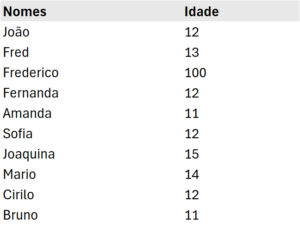
Nesse caso, caso calculássemos a média teríamos um valor médio de idade de 21 anos.
Porém nossa base não tem ninguém nessa faixa de 21 anos, e é em uma situação como essa que devemos usar a mediana, pois representará um valor mais próximo da realidade.
Para o cálculo de mediana primeiro você ordena os números do menor para o maior, porém os números que se repetem você não coloca novamente.
11, 12, 13, 14, 15, 100
Caso a contagem de números seja ímpar, basta pegar o número que se encontra no meio de todos que ele será o valor da mediana.
Caso seja par, você pega os dois números do meio, soma e divide por 2.
Como os números ordenados sem repetição são 6, vamos na segunda opção.
Pegamos os dois valores centrais (13 e 14) e somamos.
Soma dos valores centrais: 27
Divide por 2 e chegamos a uma mediana de 13 anos.
Perceba, enquanto a média nos mostrou um valor de 21 anos, a mediana já mostrou um resultado bem mais próximo da realidade.
Isso se deve por conta do outlier desse conjunto (o número 100).
Diante disso, vemos a importância de se escolher bem entre essas duas medidas.
Moda
Basicamente a moda é o valor que mais se repete dentro de um conjunto de dados, é muito útil para identificar tendências dentro de um conjunto.
Na nossa tabela acima de exemplo, conseguimos observar que o valor que mais se repete é o 12, ou seja, a idade de maior predominância na sala é 12 anos.
Medidas de dispersão
Enquanto as medidas de tendência central vão mostrar uma visão do valor típico dos dados, as de dispersão vão auxiliar no entendimento do quão espalhado ou concentrados os dados estão.
As duas principais medidas de dispersão é o Desvio Padrão e a Variância.
O desvio padrão e a variância tem uma função bem parecida, porém o desvio padrão é mais fácil de interpretar por estar na mesma escala dos valores originais.
Isso ocorre pois o desvio padrão é a raiz quadrada da variância.
Vamos usar a mesma tabela para vermos a diferença deles.
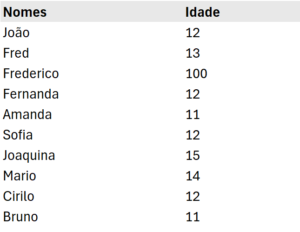
Nessa tabela temos um desvio padrão de 27.
Temos um alto valor por conta do outlier bem elevado, que influencia bastante o resultado, caso retirássemos o valor 100 teríamos um desvio de 1,33.
Enquanto isso, nossa variância é de 768, perceba como está em uma escala totalmente diferente dos valores.
Como usar a estatística descritiva para análises práticas
A estatística descritiva tem uma aplicação vasta, podendo ser usada em diversos contextos.
Por exemplo, em empresas de e-commerce, é comum usar essas ferramentas para analisar o comportamento de compra de clientes, como o valor médio das compras, faixas de preço mais frequentes, dentre outros.
Um outro bom exemplo é no marketing digital, onde a estatística descritiva ajuda a entender o tráfego de visitantes, como a quantidade média de páginas visitadas, tempo média de permanência no site, entre outros.
Além disso, vale mencionar a importância da análise gráfica na estatística descritiva.
Gráficos como histograma e boxplots são eficazes para identificar padrões, tendências e anomalias de forma visual.
Esses gráficos podem revelar por exemplo, a presença de outliers, a forma da distribuição dos dados (normal, assimétrica etc.) e ajudar a comparar diferentes conjuntos de dados.
Para maiores informações sobre gráficos, temos um artigo detalhado em https://perspectivadosdados.com/interpretacao-de-graficos-dicas-e-conceitos-essenciais/.
Conclusão
É fundamental o uso da estatística descritiva no dia a dia de um analista de dados.
Além de ser uma poderosa ferramenta para resumir dados, ela também vai te dar um excelente ponto de partida para suas análises, gerando assim insights muito mais valiosos.
Agradecemos imensamente a leitura, lembre-se de conferir nossos conteúdos em https://perspectivadosdados.com, trazemos todos os dias novos conteúdos sobre análise de dados, economia e finanças!
Recomendações de conteúdo
Estatística prática: https://amzn.to/3O5vAL6
Estatística: https://amzn.to/4fmpToj